Bayes factor (or likelihood ratio), prior probability, and posterior probability

This activity shows, for different Bayes factors (or LR), how the
​posterior probability is related to the prior probability.
A few reminders:

• posterior odds  = prior odds x BF
• To convert a probability p to odds: odds = p/(1 – p)
• To convert odds to a probability: p = odds/(1 + odds)​

​

​



























​






​





​














Posterior
​Probability

Bayes factor calculator: BF₁₀  and  BF₀₁

    P(data | H₁) = .999 .99 .95 .90 .80 // default .70 .60 .50 .40 .30 .20 .10 .05 .02 .01 .001   the probability of getting the data, given that the   alternative   hypothesis is true

    P(data | H₀) = .999 .99 .95 .90 .80 .70 .60 .50 .40 .30 .20 .10 // default .05 .02 .01 .001   the probability of getting the data, given that the   null   hypothesis is true

---

BF10 =	_____	=			BF01 =	_____	=

---

 

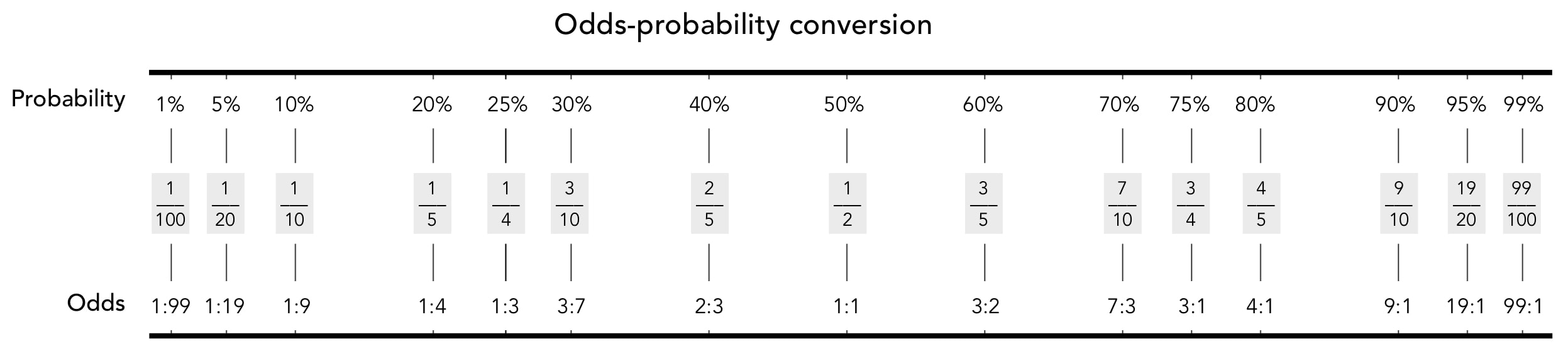
Prior-posterior plots and Bayes factors

1. Change the values in the menus above and note how the Bayes factor (or LR) changes. What produces a large Bayes factor? What produces a small Bayes factor?

2. Using the menu below, select several different Bayes factors (BF₁₀), and note how the curve changes.

3. What does a BF₁₀ (or LR) of 1 mean? Why does the curve fall on the diagonal when the Bayes factor is 1?

4. What does a BF₁₀ (or LR) of 10 mean? Why does the curve bend above the diagonal when the Bayes factor is 10?

5. For a BF₁₀ (or LR) of 4, the posterior is .80 when the prior = .50. Why? (Hint: 1 to 1 odds = probability of 1/2 or .50).

6. For a BF₁₀ (or LR) of 4, what is the posterior when the prior = .20? (Hint: 1 to 4 odds = probability of 1/5 or .20).

7. Why does the curve drop below the diagonal when BF₁₀ (or LR) = .50?

8. Suppose you did a study to test a new persuasion technique. Before the study (based on theory and previous research) you believe that there is a 30% chance that the new technique will work. The results of the study support the idea that the technique works, and the Bayes factor equals 10. Now that you know the results of the study, how sure are you that the technique works?

 

 

     BF₁₀ (or LR) = 1000 400 200 100 50 40 30 20 10 5 4 // default BF = 4 3 2 1.5 1 .80 .50 .20 .10 .05 .01 .005 .001

Prior Probability

Notes
Please email me (Burt Thompson) if you have questions or comments.
The graph is made with jQuery (query.com) and Flot (flotcharts.org).
For information about Bayes factors, see articles by Goodman (1999), Kass and Raftery (1995), Mulder and Wagenmakers (2016), and Ly et al. (2018).